最近又回了炉石坑，正好赶上发布新版本，但是由于2年多没玩落后了太多版本，这期间出了不少的卡牌，于是买了个预购100包追一下版本（因为穷没舍得再买了）。对于我这个收集玩家来说，还差了不少卡牌，于是就突然想计算下，究竟集齐卡牌需要开多少包。
首先，得弄清炉石的开包机制是什么，因为炉石卡牌是可以无限收集的，那么我猜想的抽取到同等品质的卡牌就类似于投掷多面的均匀骰子，这样在数量非常大的情况下，是满足均匀分布的。
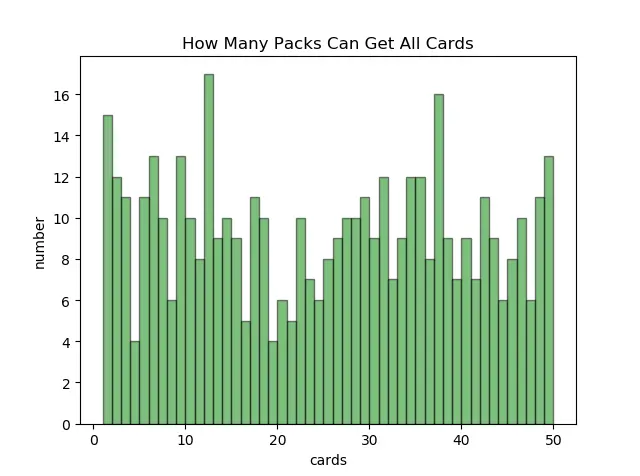
使用炉石盒子进行了卡牌的统计后，发现无缺失卡牌，并且每张都有两张以上，然后按照白卡抽到概率相同，模拟了白卡的统计直方图，发现和盒子统计的数据基本一致。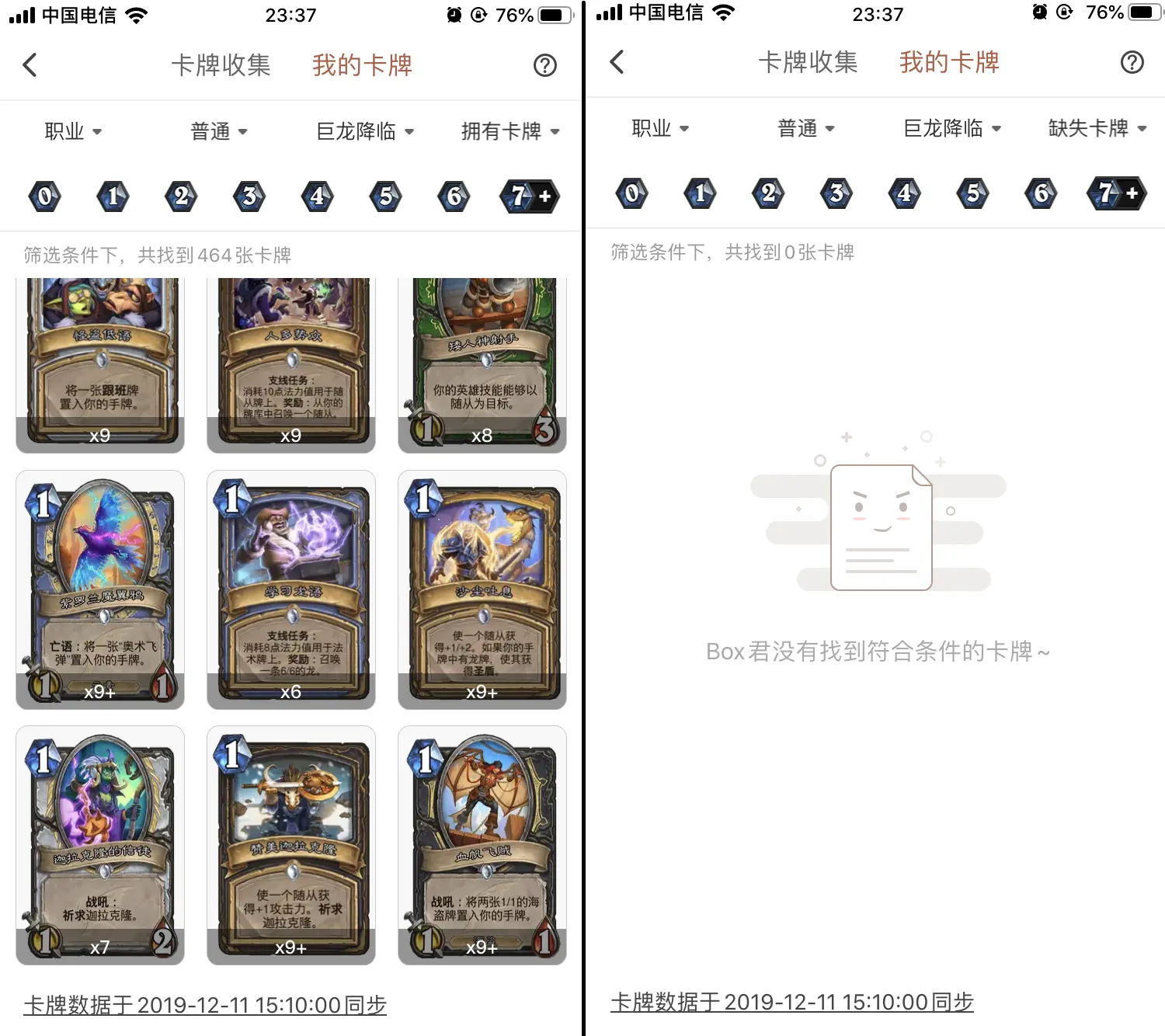
于是，问题就变成了卡牌收集问题，而卡牌收集问题其实类似如下问题： 1.抛多少次硬币才能正反面各出现一次。 2.抛多少次骰子才能每个点数各出现一次。 3.优惠券收集者问题：如果每个盒子都包含一个优惠券，并且总共有n种不同类型的优惠券，那么需要少盒子才能能购买到全部n个优惠券？
在概率论经典问题优惠券收集者问题中，数学家们给出了求解：
设$T$为收集到所有N个优惠券需要的次数，$t_{i}$为收集$i − 1$ 个优惠券后收集第i个优惠券的次数。将$T$和$t_{i}$视为随机变量。观察到收集新优惠券的概率为 ${\displaystyle p_{i}={\frac {n-i+1}{n}}}$。因此， ${\displaystyle t_{i}}$ 具有期望的几何分布 ${\displaystyle {\frac {1}{p_{i}}}}$。通过期望的线性，我们有：
$${\displaystyle {\begin{aligned}\operatorname {E} (T)&=\operatorname {E} (t_{1})+\operatorname {E} (t_{2})+\cdots +\operatorname {E} (t_{n})={\frac {1}{p_{1}}}+{\frac {1}{p_{2}}}+\cdots +{\frac {1}{p_{n}}}\\&={\frac {n}{n}}+{\frac {n}{n-1}}+\cdots +{\frac {n}{1}}\\&=n\cdot \left({\frac {1}{1}}+{\frac {1}{2}}+\cdots +{\frac {1}{n}}\right)\\&=n\cdot H_{n}.\end{aligned}}}$$这里$H_{n}$是第N次谐波数。利用谐波数的渐近性，我们得到：
$${\displaystyle \operatorname {E} (T)=N\cdot H_{n}=N\ln n+\gamma N+{\frac {1}{2}}+O(1/n)}$$其中${\displaystyle \gamma \approx 0.5772156649}$是欧拉-马斯切罗尼常数。
当然，炉石只有橙卡满足式一，其余的卡牌我们都需要收集两张。Donald J. Newman和Lawrence Shepp给出了优惠券收集者问题中，收集全套优惠券m份的推广形式。令$T_{m}$为第一次收集每张优惠券的m份，他们表明在这种情况下的期望可以满足：
$$ {E} (T_{m})=N(\ln N+(m-1)\ln \ln N+C_{m})+{\frac {1}{2}}+O(n)$$其中$C_{m} = \gamma - ln(m-1)!$
在巨龙降临全卡中，共有246张卡，其中
$${\mathbf{表1-卡牌统计}}$$| 普通 | 稀有 | 史诗 | 传说 |
|---|---|---|---|
| 49*2 | 36*2 | 27*2 | 22+6(赠卡) |
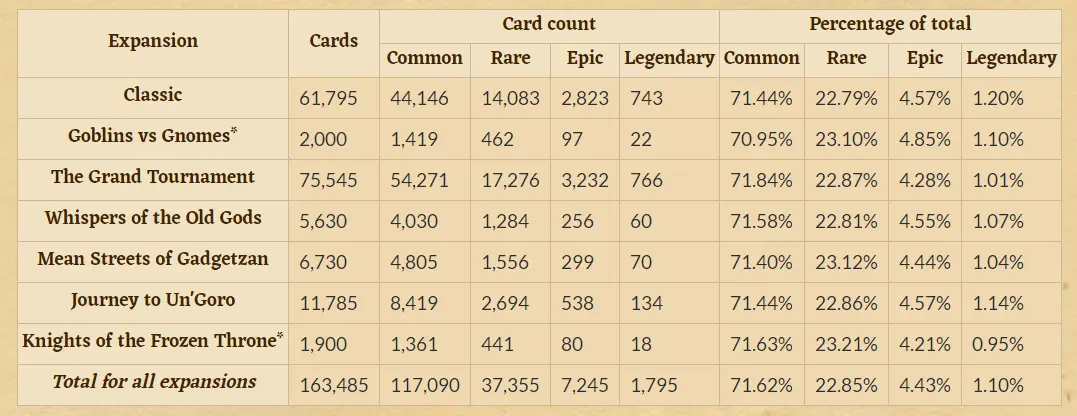
在开卡包过程中，必有一张卡牌是稀有，其余卡牌根据概率出现，我们根据GAMEPEDIA网站开包数据统计，可以得到每种品质的卡牌的平均出现概率，我认为样本量应该是足够的。
去除2000（400包）以下的开包数据（可能有点少），计算各品质平均出现概率如表2第一行所示。表3第二行是对其四舍五入得到一个近似概率，基本是我们在样本量足够的情况下，每张卡出现品质的概率。这也解释了，一般情况下下（若脸不黑），40包（200张卡牌）一般是能开出来两张传说的，$200 * 0.011 \approx 2$ 。
$${\mathbf{表2-各品质卡牌平均出现概率}}$$| 普通 | 稀有 | 史诗 | 传说 |
|---|---|---|---|
| 71.54% | 22.89% | 4.482% | 1.092% |
| 71.5% | 22.9% | 4.5% | 1.1% |
有了卡牌平均出现概率，就很好计算集齐每种品质所需要的平均卡包数量了。通过计算期望我们可以得到平均抽多少张卡牌才能集齐该品质的全卡(除橙卡外各两张)。以白卡为例，平均需要抽到286张普通，才能使每张普通都有两张，其余数据见表3
$${\mathbf{表3-集齐各品质卡牌期望}}$$| 期望/质量 | 普通 | 稀有 | 史诗 | 传说 |
|---|---|---|---|---|
| 卡牌数量 | 286.06 | 196.23 | 137.27 | 106.02 |
根据集齐卡牌数量的期望，我们通过卡牌出现的概率，可以计算出总共多少张卡牌能达到期望的数量。如普通卡牌，可以得到 $N = \frac{286.0677}{0.715} = 400.0946$，计算结果如表4。
$${\mathbf{表4-集齐各品质卡牌需要卡包数量}}$$| 全卡期望/质量 | 普通 | 稀有 | 史诗 | 传说 |
|---|---|---|---|---|
| 卡牌数量 | 400.09 | 856.92 | 3,050.53 | 7,381.97 |
| 卡包数量 | 80.01 | 171.38 | 610.10 | 1,476.39 |
很显然，若不用粉尘的情况下，平均需要开1,476包才能得到全部的卡牌。
根据得到全卡史诗的期望，平均需要610包，共3050张卡牌，根据表2各品质卡牌出现概率，计算出分解粉尘期望，如表5所示：
$${\mathbf{表5-关于粉尘}}$$| 粉尘/质量 | 普通 | 稀有 | 史诗 | 传说 | 总计 |
|---|---|---|---|---|---|
| 全卡合成所需粉尘 | 3,920 | 7,200 | 21,600 | 35,200 | 67,920 |
| (171包)多余卡牌分解粉尘 | 2,573.49 | 2,484.69 | ？ | ？ | >5,058.18 |
| (610包)多余卡牌分解粉尘 | 10,415.67 | 12,531.46 | 33,309.67 | ？ | >56,256.81 |
可以看出，610包开完后，可以合成全部橙卡，还多出2W多粉尘。那么区间大致缩小在171~610包即可获得巨龙降临全卡。
根据hearthsim.info绘制出的有效粉尘期望和分解粉尘期望图，可以看出，在150包之后，平均分解粉尘期望在55以上，获得期望价值粉尘大概平均为165（猜的）。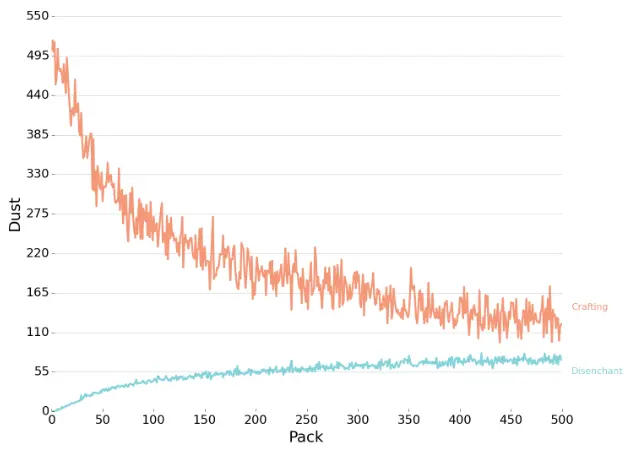
那么假设171包中，史诗开出$171 * 5* 0.045 \approx 38$ 张，且都没有超过2张，橙卡为$171 *5 * 0.011 \approx 9$张，且无重复 ，接下来将剩余史诗和橙卡所需的粉尘加起来，除以期望价值粉尘，大概为165包（理想情况，应该更多）。这种情况下，预计336包（165+171）能利用粉尘集齐全部卡牌。
假设卡牌全部收集到后，每包卡牌分解粉尘期望值为: $ 5 * (0.715 * 5 +0.229 * 10 + 0.045 * 100 + 0.011 * 400) = 73.825$ 观察粉尘期望图中的分解曲线，发现基本在350~500包中，期望粉尘大致拟合在一条直线上大概在70-80，说明卡牌基本集齐了。
结论：预计在400包内，利用分解粉尘，可集齐巨龙降临全部卡牌。
参考
[1]双迪克西杯问题
[2]https://hearthstone.gamepedia.com/Card_pack_statistics
[3]https://en.wikipedia.org/wiki/Coupon_collector’s_problem
[4]https://hearthsim.info/blog/the-grand-tournament-card-pack-opening