一、进食前提
这里需要了解Encoder–Decoder模型
二、Transformer模型概览

三、模型细节
1. 输入文本的向量化
假设我们翻译一句话
我们将词向量与位置编码(Positional Encoding)相加输入
为什么加入位置编码?
原文翻译:由于我们的模型不包含递归和卷积,为了让模型利用序列的顺序,我们必须注入一些关于序列中标记的相对或绝对位置的信息。为此,我们将“位置编码”添加到编码器和解码器堆栈底部的输入嵌入中。位置编码具有与嵌入相同的维数模型,因此可以将两者相加。有多种固定位置,学习,编码的选择。在这项工作中,我们使用不同频率的正弦和余弦函数: Positional Encoding实现参考
$$P E_{(p o s, 2 i)}=\sin \left(p o s / 10000^{2 i / d_{\text {madd }}}\right)$$ $$P E_{(p o s, 2 i+1)}=\cos \left(p o s / 10000^{2 i / d_{\text {madd }}}\right)$$3.1 Encoder
2 Multi-Head Attention
2.1 Scaled Dot-Product Attention
我们先来看Scaled Dot-Product Attention,公式表达如下
$$ \text { Attention }(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V $$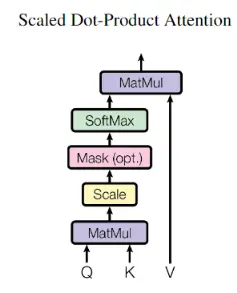
具体计算过程
从编码器的每个输入向量创建三个向量。因此,对于每个单词,我们创建一个查询向量、一个关键字向量和一个值向量。这些向量是通过将嵌入向量乘以我们在训练过程中训练的三个矩阵来创建的。他们的维度为64
1.$X_{i}$乘以权重矩阵$W^{Q},W^{K},W^{V}$产生$q_{i},k_{i},v_{i}$
$$q_{i} = W^{Q}*x_{i}$$ $$k_{i} = W^{K}*x_{i}$$ $$v_{i} = W^{V}*x_{i}$$2.得分是通过将查询向量与我们正在评分的相应单词的关键向量的点积计算出来的。因此,如果我们正在处理位置为$pos1$的单词,第一个分数是$q_{1}$和$k_{1}$的点积。第二个分数将是$q_{1}$和$k_{2}$的点积。
$$Score=q_{posi}*k_{i}$$3.将每个除以$\sqrt{d_{k}}$ 4.应用Softmax函数来获得值的权重。 5.将每个值向量乘以Softmax得分
$$v_{i}{'}=v_{i}*softmax_{i}$$6.对加权值向量进行求和
$$z_{1}=v_{1}{'}+v_{2}{'}+...+v_{i}{'}$$2.2 Multi-Head Attention
Multi-Head Attention的公式表达如下
$$ \begin{aligned} \text { MultiHead } (Q, K, V) &=\text { Concat } \left(\text { head }_{1}, \ldots, \text { head }_{\mathrm{h}}\right) W^{O} \\ \text { where head }_{\mathrm{i}} &=\text { Attention }\left(Q W_{i}^{Q}, K W_{i}^{K}, V W_{i}^{V}\right) \end{aligned} $$Multi-Head Attention的计算过程
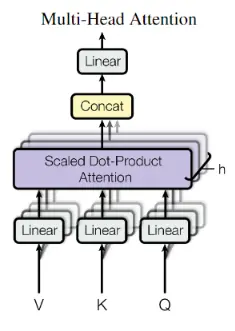 先看一下计算过程
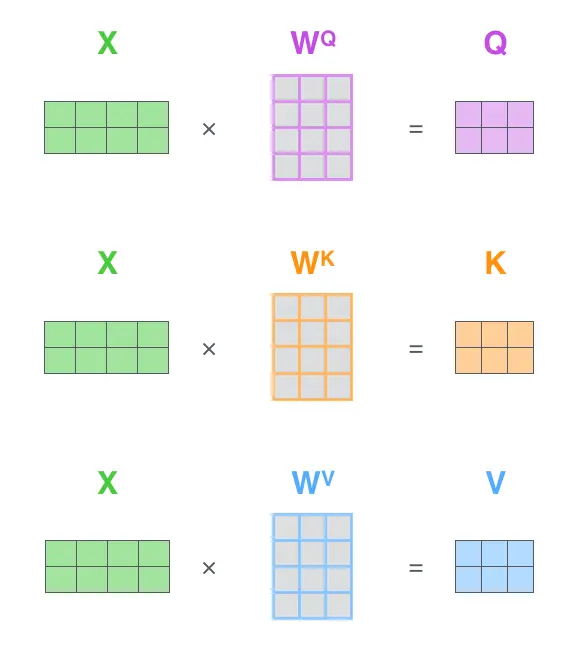
先看一下计算过程1.将单词转为512维度的词向量 2.Q,K,V矩阵的计算 这里X矩阵向量为512(用横向4个格子表示),Q,K,V矩阵向量为64(用横向3个格子表示)
 2.计算自我注意层的输出
2.计算自我注意层的输出3.论文中使用8个(h=8)平行的注意力层(Scaled Dot-Product Attention),所以我们计算出由$Q_{0}…Q_{7},K_{0}…K_{7},V_{0}…V_{7}$组成的8组$(Q_{i},K_{i},V_{i})$组成的矩阵 $d_{k}=d_{v}=d_{model}/h$=64


到这里,终于把Encoder和Decoder共有的Multi-Head Attention层理解完了。接下来我们看经过attention后是如何进行的
2.3.Add & Layer-Normalization
通过残差连接和层正则化,计算出新的$Z_{i}$,依次传递到下一层,直到最后一层输出
$$ \mathrm{FFN}(x)=\max \left(0, x W_{1}+b_{1}\right) W_{2}+b_{2} $$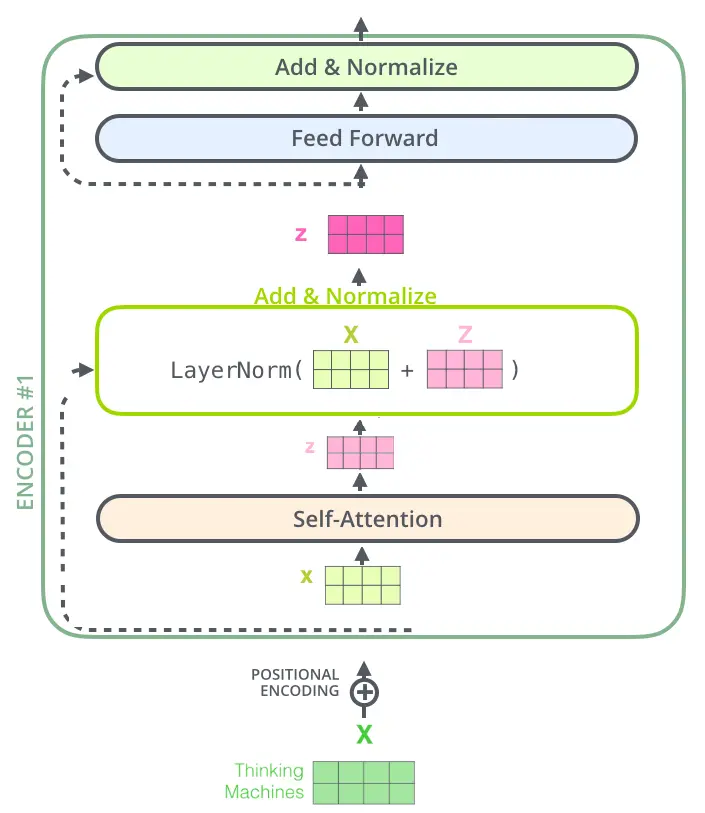
3.2 Decoder
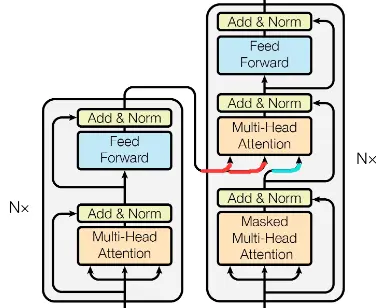
接下来将最后输出的向量拼接成矩阵Z,然后分别输入到每一层的Multi-Head Attention层,生成$K,V$矩阵,因为每一层的Multi-Head Attention都一样,所以简化至下图,即$K,V$矩阵依次输入到各个Decoder
Multi-Head Attention层有三个输入,如下图所示,两个是由Encoder输入的,另一个是由Decoder底层的Masked Multi-Head Attention输入的(分别用红线和蓝线标明)。
接下来的概率输出
最终的Linear层和Softmax层
线性层是一个简单的完全连接的神经网络,它将解码器堆栈产生的向量投影到一个更大的向量中,称为logits向量。 模型输出时,假设模型知道从其训练数据集中学习的10,000个独特的英语单词(输出词汇)。这将使logits矢量10,000个单元格-每个单元格对应于一个唯一单词的分数,Softmax层将这些分数转换为概率(全部为正数,合计为1.0)。选择具有最高概率的单元格,并产生与其相关联的单词作为该时间步长的输出。
即输出 I am a student
若有些理解不到位和不足的地方,请多多指教!
参考文章
[1] Attention Is All You Need
[2] The Illustrated Transformer
[3] Add & Layer-Normalization
[4] Transformer模型的学习总结










