一、进食前提
这里要弄明白RNN,LSTM,BiRNN,Seq2Seq
二、RNN With Encoder-Decoder
在Encoder-Decoder框架中,编码器读取输入语句,即向量序列$\mathbf{x}=\left(x_{1}, \cdots, x_{T_{x}}\right)$,生成中间语义向量$c_{i}$
我们先看一个大概的流程
$c$当作 Decoder 的每一时刻输入,则是 Seq2Seq 模型的第一种模型:
如果直接将$c$ 输入到 Decoder 中,则是 Seq2Seq 模型的第二种模型:
即我们要在Encoder内计算隐状态$h_{i}$ ,最后得到中间语义向量$c$,将其送入Decoder,再由Decode进行解析,输出每次对应的$y_{i}$在其先验条件下的输出概率最大的词。
从目前来看,我们仅需知道三个参数$h_{t}$,$c$,$s_{t}$就可以进行翻译了
该论文最后给出了两种实现模型,通用框架A1和 A2
我们可以将翻译步骤略缩为①和②
①Encoder部分
当前的隐层输出$h_{t}$由上一层的隐层输出$h_{t-1}$和当前层输入$x_{t}$计算得出
$$h_{t}=f\left(x_{t}, h_{t-1}\right) \tag{1}$$这里对于RNN的激活函数$f$,作者使用Choet 等人(2014a) 1提出的门控隐藏单元。
再通过计算得到中间语义向量$c$
$$c=q\left(\left\{h_{1}, \cdots, h_{T_{x}}\right\}\right)$$接下来将中间语义向量$c$送入Decoder
②Decoder部分
给出了定义的条件概率,用以计算$y_{i}$在当前时刻输出概率最高的词语
$$p\left(y_{i} | y_{1}, \ldots, y_{i-1}, \mathbf{x}\right)=g\left(y_{i-1}, s_{i}, c_{i}\right) \tag{3}$$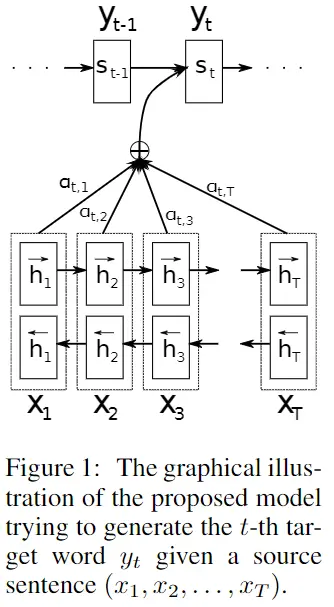
大概结构和流程搞清楚后,进入Encoder部分,$h_{t}$计算方法已经给出,来看看剩下的个参数是如何计算得出的
一、论文提出的第一种通用框架A1
A1 Encoder
$c_{i}$ 由权重 $\alpha_{i j}$ 和 隐层输出$h_{i}$ 计算加权和得到
$$c_{i}=\sum_{j=1}^{T_{x}} \alpha_{i j} h_{j}\tag{4}$$每个注释$h_{i}$的权重$\alpha_{i j}$通过下式计算
$$\alpha_{i j}=\frac{\exp \left(e_{i j}\right)}{\sum_{k=1}^{T_{x}} \exp \left(e_{i k}\right)} \tag{5.1}$$$e\left(y_{i-1}\right) \in \mathbb{R}^{m}$ 是单词$y_{i-1}$的K维(1-K)的词向量嵌入,$e\left(y_{i}\right)$为$m * K$ 的嵌入矩阵 $E \in \mathbb{R}^{m \times K}$ ,$r_{i}$是复位门的输出。论文里忽略了偏差项,使方程变得更简洁。
$$e_{i j}=a\left(s_{i-1}, h_{j}\right) \tag{5.2}$$对于长度为$T_{x}$和$T_{y}$的每个句子,设计对齐模型时应考虑需要评估模型$T_{x}$×$T_{y}$次,为了减少计算,使用单层多层感知器
$$a\left(s_{i-1}, h_{j}\right)=v_{a}^{\top} \tanh \left(W_{a} s_{i-1}+U_{a} h_{j}\right)\tag{5.3}$$$v_{a} \in \mathbb{R}^{n’}$ $W_{a} \in \mathbb{R}^{n’ \times n}$ $U_{a} \in \mathbb{R}^{n’ \times 2n}$ 为权重矩阵,由于$U_{a}$和$h_{j}$ 不依赖于$i$,我们可以对其进行预先计算以最大程度地减少计算成本
A1 Decoder
利用解码器状态$s_{i-1}$,上下文$c_{i}$和最后生成的单词$y_{i-1}$,我们将目标单词yi的概率定义为
$$p\left(y_{i} | y_{1}, \ldots, y_{i-1}, \mathbf{x}\right)=g\left(y_{i-1}, s_{i}, c_{i}\right) \tag{6}$$$s_{i}$为图一上面部分RNN结构i时刻隐层的状态
$$s_{i}=f\left(s_{i-1}, y_{i-1}, c_{i}\right)\tag{7.1}$$公式的展开
$$f\left(s_{i-1}, y_{i-1}, c_{i}\right)=\left(1-z_{i}\right) \circ s_{i-1}+z_{i} \circ \tilde{s}_{i} \tag{7.2}$$ $$\tilde{s}_{i}=\tanh \left(W e\left(y_{i-1}\right)+U\left[r_{i} \circ s_{i-1}\right]+C c_{i}\right)\tag{7.3}$$ $$z_{i}=\sigma\left(W_{z} e\left(y_{i-1}\right)+U_{z} s_{i-1}+C_{z} c_{i}\right) \tag{7.4}$$ $$r_{i}=\sigma\left(W_{r} e\left(y_{i-1}\right)+U_{r} s_{i-1}+C_{r} c_{i}\right) \tag{7.5}$$权重矩阵:$W, W_{z}, W_{r} \in \mathbb{R}^{n \times m}$ $U, U_{z}, U_{r} \in \mathbb{R}^{n \times n}$ $C, C_{z}, C_{r} \in \mathbb{R}^{n \times 2 n}$
where ◦ is an element-wise multiplication,即该符号代表点积 where σ (·) is a logistic sigmoid function,即该符号代表sigmoid函数
更新门$z_{i}$允许每个隐藏单元保持其先前的激活状态
二、论文提出的第二种模型 A2
A2 Encoder
输入 1-of-K 词向量 $\mathbf{x}=\left(x_{1}, \ldots, x_{T_{x}}\right), x_{i} \in \mathbb{R}^{K_{x}}$ 输出 1-of-K 词向量 $\mathbf{y}=\left(y_{1}, \ldots, y_{T_{y}}\right), y_{i} \in \mathbb{R}^{K_{y}}$ 其中$K_{x}$和$K_{y}$分别是源语言和目标语言的词汇量。
首先,计算双向递归神经网络(BiRNN)的前向状态
$$\overrightarrow{h}_{i}=\left\{\begin{array}{ll}{\left(1-\overrightarrow{z}_{i}\right) \circ \overrightarrow{h}_{i-1}+\overrightarrow{z}_{i} \circ \overrightarrow{\underline{h}}_{i}} & {, \text { if } i>0} \\ {0} & {, \text { if } i=0}\end{array}\right. \tag{8.1}$$ $$\overrightarrow{\underline{h}}_{i}=\tanh \left(\overrightarrow{W} \overline{E} x_{i}+\overrightarrow{U}\left[\overrightarrow{r}_{i} \circ \overrightarrow{h}_{i-1}\right]\right) \tag{8.2}$$ $$\overrightarrow{z}_{i}=\sigma\left(\overrightarrow{W}_{z} \overline{E} x_{i}+\overrightarrow{U}_{z} \overrightarrow{h}_{i-1}\right)\tag{8.3}$$ $$\overrightarrow{r}_{i}=\sigma\left(\overrightarrow{W}_{r} \overline{E} x_{i}+\overrightarrow{U}_{r} \overrightarrow{h}_{i-1}\right)\tag{8.4}$$ $$\overline{E} \in \mathbb{R}^{m \times K_{x}}是词向量矩阵,\overrightarrow{W}, \overrightarrow{W}_{z}, \overrightarrow{W}_{r} \in \mathbb{R}^{n \times m} \overrightarrow{U},\overrightarrow{U}_{z}, \overrightarrow{U}_{r} \in \mathbb{R}^{n \times n}$$反向传播状态 \(\left (\overleftarrow{h}_{1} \cdots \overleftarrow{h}_{T_{x}} \right)\) 计算与上面相似,与权重矩阵不同,我们在前向传播和反向传播RNN之间共享单词嵌入矩阵 \(\overline{E}\),将前向传播和反向传播状态连接起来得到 \($\left({h}_{1},{h}_{2}, \ldots, {h}_{T_{x}}\right)\)
$$\begin{bmatrix} \overrightarrow{h}_{i}\\ \overleftarrow{h}_{i} \end{bmatrix} \tag{9}$$A2 Decoder
给出了定义的条件概率,用以计算$y_{i}$在当前时刻输出概率最高的词语
$$p\left(y_{i} | y_{1}, \ldots, y_{i-1}, \mathbf{x}\right)=\propto exp\left ( y_{i}^{\top }W_{o}t_{i} \right )\tag{3}$$ $$t_{i} = \left [ max\left \{ \tilde{t}_{i,2j-1},\tilde{t}_{i,2j} \right \} \right ]_{j=1,\dots,l}^{\top } \tag{4}$$ $$\tilde{t}_{i}= U_{o}s_{i-1}+V_{o}Ey_{i-1}+C_{o}c_{i}\tag{5}$$解码器的隐藏状态$s_{i}$,是通过编码器给出的注释经过计算得到的(应该是这个意思)
注意,这里计算公式与上面的A1在细节有差异了 公式的展开
$$s_{i}=\left(1-z_{i}\right) \circ s_{i-1}+z_{i} \circ \tilde{s}_{i} \tag{7.2}$$ $$\tilde{s}_{i}=\tanh \left(W Ey_{i-1}+U\left[r_{i} \circ s_{i-1}\right]+C c_{i}\right)\tag{7.3}$$ $$z_{i}=\sigma\left(W_{z} Ey_{i-1}+U_{z} s_{i-1}+C_{z} c_{i}\right) \tag{7.4}$$ $$r_{i}=\sigma\left(W_{r} Ey_{i-1}+U_{r} s_{i-1}+C_{r} c_{i}\right) \tag{7.5}$$$E$是目标语言的单词嵌入矩阵,权重矩阵:$W, W_{z}, W_{r} \in \mathbb{R}^{n \times m}$ $U, U_{z}, U_{r} \in \mathbb{R}^{n \times m}$ $C, C_{z}, C_{r} \in \mathbb{R}^{n \times 2n}$,m和n是词的嵌入维数和隐藏单位数
where ◦ is an element-wise multiplication,即该符号代表点积 where σ (·) is a logistic sigmoid function,即该符号代表sigmoid函数
初始隐藏状态$s_{0}$ = $tanh\left( W_{s}\overleftarrow h_{i}\right)$,$W_{s} \in \mathbb{R}^{n \times n}$
参考
[1] Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation. arXiv:1406.1078v3 (2014).
[2] Sequence to Sequence Learning with Neural Networks. arXiv:1409.3215v3 (2014)
[3] Visualizing A Neural Machine Translation Model (Mechanics of Seq2seq Models With Attention)
[4] 详解从 Seq2Seq模型、RNN结构、Encoder-Decoder模型 到 Attention模型



