LLM - Learning Tips | MakiNaruto's Blog

模型参数量的计算

数据精度

要计算参数量, 我们首先要知道, 在计算机表示中, 对于数据的表示精度范围不同, 意味着该数据表示形式可能占用的内存空间也不同.
浮点数在计算机中的存储分为三个部分：
　1. 符号位（sign）：float和double符号位均为1位，0代表正数，1代表负数
　2. 指数位（exponent）：存储科学计数法中的指数部分，采用移位存储
　3. 尾数位（fraction）：存储科学计数法中的尾数部分

$$(-1)^{符号位} \times 2^{指数位 - 指数偏移} \times (1 + \frac{尾数位}{1024}) $$

例如fp16, 举例说明:
　Exponent(指数位)：5
　　表示范围 00001(1)到11110(30)
　　为了能表示负数，减去偏置（15），指数部分（-14 - 15 ）
Fraction 位数位：10
　　共10位
　　表示范围 0000000000 - 1111111111（ 0~1023）
　　除以1024（0 - 1023）/1024

可以表示的最大数据(符号位=1，指数位=30，尾数位=1）：
$(-1)^{0} \times 2^{30 - 15} \times (1 + \frac{1023}{1024}) $
可以表示的最小数据(符号位=-1，指数位=30，尾数位=1）：
$(-1)^{1} \times 2^{30 - 15} \times (1 + \frac{1023}{1024}) $

常用数据精度

简称	全称	符号位	指数位	小数位	总位数	字节数	表示范围
fp32	单精度浮点数（Single-precision floating-point）	1	8	23	32	4	$[-3.4 × 10^{38}, 3.4 × 10^{38}]$
fp16	半精度浮点数（Half-precision floating-point）	1	5	10	16	2	$[-65504, 65504]$
bf16	Brain 浮点数（Brain floating-point）	1	8	7	16	2	$[-3.39 × 10^{38}, 3.39 × 10^{38}]$

计算

比如一个14B的模型, 其中所有的数据精度都为fp16(16位, 2byte). 那么加载模型时, 先进行单位换算, 1 byte = 8 bits
1 KB = 1,024 bytes
1 MB = 1,024 KB
1 GB = 1,024 MB

因为每个数据精度都为fp16, 占2字节, 所以需要先乘以2. 计算公式为:
1,400,000,000 * 2 / 1024 / 1024 / 1024 ≈ 1,400,000,000 * 2 / $10^{9}$ ≈ 28G

由此, 以B为单位的模型, 可以直接进行粗略计算, 使用字节数 * 前面的数字, 计算单位为G. 比如一个 14B 的大模型, 以fp16方式加载后, 预计推理需要的显存大小为: 14 * 2 = 28G

Loss图像

常见激活函数的图像:

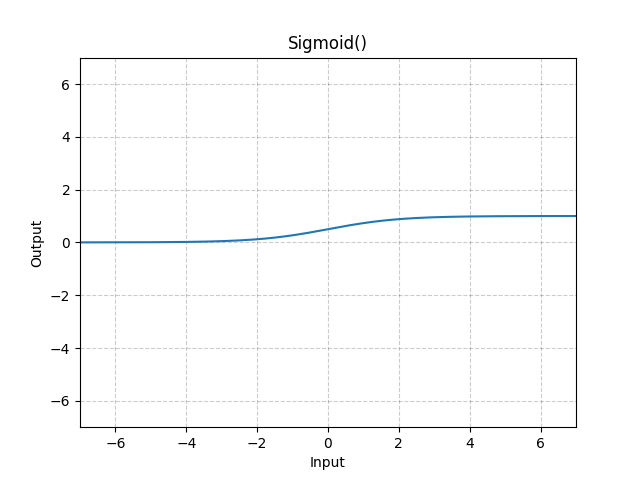
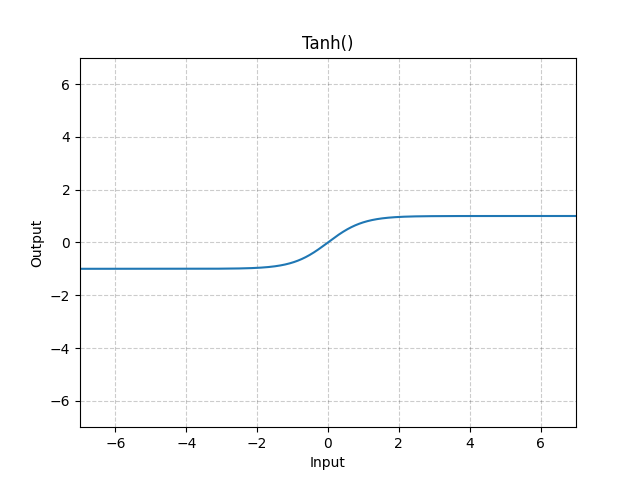
其他激活函数: non-linear-activations

LoRA

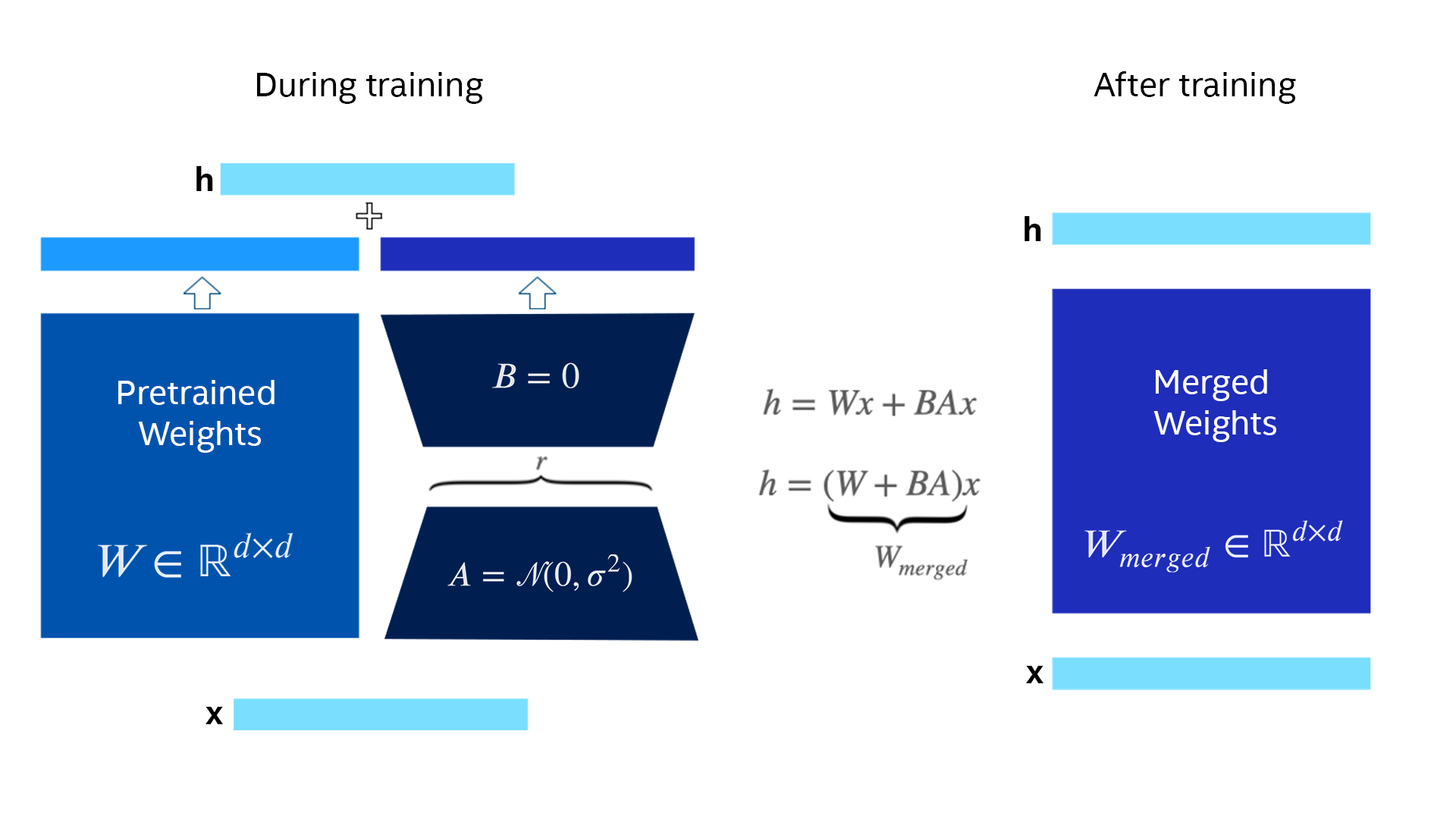
LoRA加速原理

比如有非常大维度的权重矩阵 W, 其维度为1024x2048.

首先，我们将这个权重矩阵冻结，即不再对其进行更新。
引入低秩矩阵: 我们用两个更小的矩阵A, B 代替 W. A: 1024x32，B: 32x2048。
计算新的输出: 在进行前向传播时，我们将输入向量先与A相乘，得到一个维度为32的中间向量。然后，将这个中间向量与B相乘，得到最终的输出。这个过程可以表示为：
output = input @ A @ B
训练低秩矩阵: 在训练过程中，我们只更新A和B这两个小矩阵的参数，而原始的权重矩阵保持不变。由于A和B的维度远小于原始的权重矩阵，因此训练速度会大大加快。
训练结束后合并矩阵: 将更新加到原始权重矩阵: 将计算得到的 ΔW 加到原始的权重矩阵 W 上，得到新的权重矩阵 W’：
ΔW = A @ B
W’ = W + ΔW
也就是当我们训练完毕推理时, 使用的为合并后的矩阵.

LoRA只操作模型的线性层, 并且一般不会对lm_head进行参数的更新.

训练期间和训练后的 LoRA 示意图:

将 LoRA 权重合并到基础模型中

embedding

大模型本身是有embedding层的, 不需要去再加载一些单独训练的embedding了, 其embedding的维度和字典的维度不相同. 但在传统的Word2vec、bert等模型中, 其embedding是与字典的长度相同的. 为什么会有这个差异?

1model.base_model.embed_tokens
2>>> Embedding(151936, 896)
3tokenizer.vocab_size
4>>> 151643

特殊token: 除了常规的词汇，模型通常还会引入一些特殊的token，比如、、等。这些token虽然不在原始的词表中，但也会被分配一个embedding向量，从而导致embedding层的维度略大于词表长度。
预留空间: 在模型训练过程中，为了应对新的词汇或者一些特殊的需求，模型可能会预留一些额外的embedding向量。这些预留的向量可以用来表示未出现在训练数据中的词，或者用于一些特定的任务。
模型架构设计: 某些模型架构可能会在embedding层上进行一些额外的操作，比如引入位置编码等。这些操作可能会导致embedding层的维度发生变化。

attention_mask 的作用

1# 生成随机输入和掩码
2X = torch.randn(5, 3)
3mask = torch.tensor([[1, 1, 0], [1, 0, 0], [1, 1, 1], [0, 0, 0], [1, 0, 1]])

当我们将一些信息选为不关注时, 对信息的关注也是不同的, 如下图所示:

LLM - Learning Tips