画图
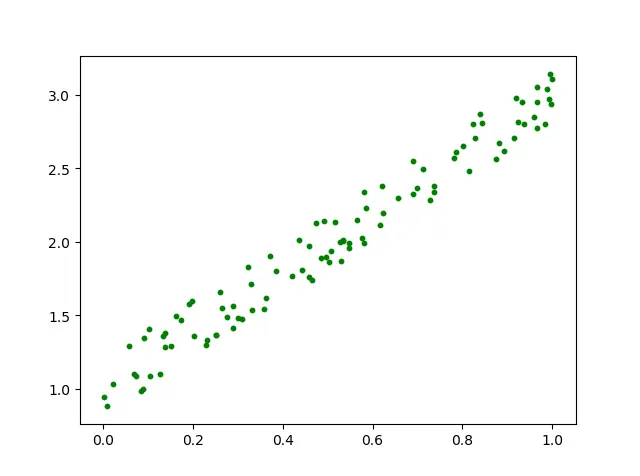
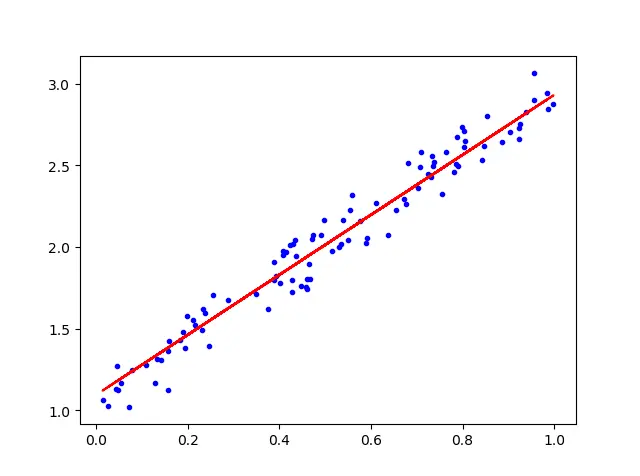
让我们以直线 y=2x+1 附近作散点图,误差内上下浮动。
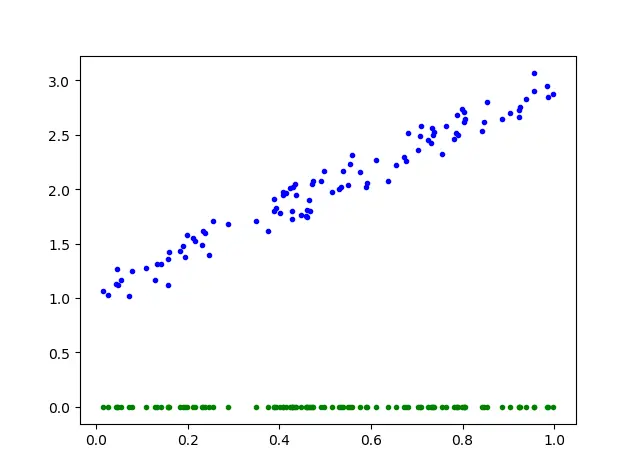
因为开始时,截距$\theta_{0}$和斜率$ \theta_{1}$初始都为0,绿点为初始点的分布。所以将其描点如图所示。
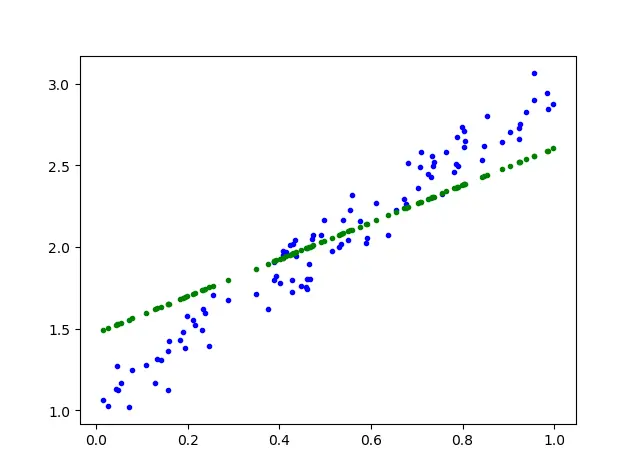
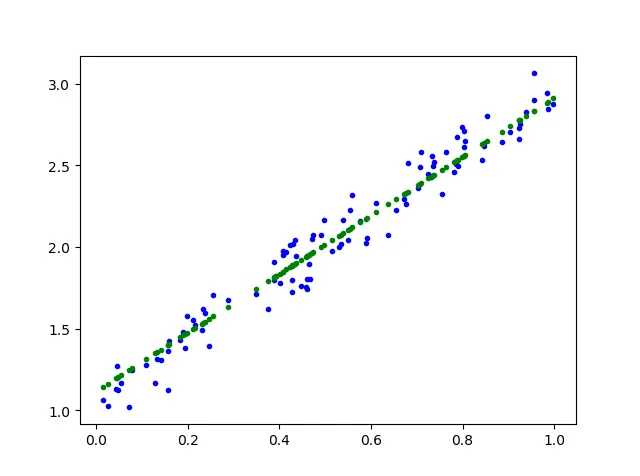
简单用三幅图表示学习过程
$$h_{\theta}(x)=\theta_{0}+\theta_{1} x \tag{1}$$$$ J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{2 m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)^{2} \tag{2}$$很明显,公式①一元线性表达式就是我们常用的 $y = b + ax \tag{3}$
我们的目的是使代价函数尽可能的小:$ \underset{\theta_{0}, \theta_{1}}{\operatorname{minimize}} J\left(\theta_{0}, \theta_{1}\right)\tag{4}$
接下来我们开始工作,进行梯度下降用到了求偏导。当对其进特征,也就是对$\theta_{0},\theta_{1}$求偏导。每次求偏导后更新公式为
$\theta_{0} :=\theta_{0}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right)\tag{5}$
$\theta_{1} :=\theta_{1}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \cdot x^{(i)}\tag{6}$
那么将公式(1) 一元元线性表达带入式子(5) 得到式子(7):
$$\theta_{0} :=\theta_{0}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left((\theta_{0}+\theta_{1} x)-y^{(i)}\right)\tag{7}$$在式(7)中,我们将$(\theta_{0}+\theta_{1} x)-y^{(i)}$ 抽取出来,暂时定义$y^{(d)} = \theta_{0}+\theta_{1} x$,这个就是我们正在变化的绿点,其横坐标$x$不会变化,这样就很明显,每一个蓝点都有对应的绿点在其垂直于$x$轴的连线上,且绿点通过学习不断的变动垂直距离上的位置,我们把公式(7)换一种表达方式,引入$y^{(d)}$
$\theta_{0} :=\theta_{0}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(y^{(d)}-y^{(i)}\right)\tag{8}$
这样一看,我们很清楚的就能得到平均垂直距离,也就是$y^{(d)}$随之每次学习,$\theta_{0}$一点一点的变大,蓝点与绿点的垂直距离越来越小,$\theta_{0}$的变化也逐渐变小直至稳定,$\theta_{1}$同理。
代码如下
1import numpy as np
2import matplotlib.pyplot as plt
3import random
4
5X = np.random.random(100).reshape(100,1) #随机生成100行1列的随机值
6Y = np.zeros(100).reshape(100,1)
7for i , x in enumerate(X):
8 val = x * 2 + 1 + random.uniform(-0.2,0.2)
9 Y[i] = val # 令y的值随机偏动在范围内
10
11plt.figure()
12plt.scatter(X,Y,color='g',s=10) #X1 为横坐标轴值,y为纵坐标值
13# plt.plot(X,2 * X + 1,color='r',linewidth=2.5,linestyle='-')
14plt.show()
执行梯度下降以进行线性回归的代码段
1#最小二乘法,用来计算损失
2def compute_error(theta0,theta1,x_data,y_data):
3 totalError=0
4 for i in range(0,len(x_data)):
5 totalError += ( (theta0 + theta1 * x_data[i]) - y_data[i] ) ** 2
6 return totalError/float(len(x_data))
7
8#梯度下降法
9def gradient_descent_runner(x_data,y_data,Theta0,Theta1,lr,epochs):
10 #计算数据总量长度
11 m = float(len(x_data))
12 J_Cost = {}
13 #循环epochs
14 for i in range(epochs):
15 J_Theta0 = 0
16 J_Theta1 = 0
17 J_CostValue = 0
18 #每迭代5次,输出一次图像
19 if i % 50 == 0:
20 print("epochs",i)
21 plt.plot(x_data,y_data,'b.')
22 plt.plot(x_data, Theta1 * x_data + Theta0 ,'g.')
23 plt.show()
24 pass
25 pass
26 '''
27 repeat until convergence{
28 start
29 '''
30 #计算梯度
31 for j in range(0,len(x_data)):
32 #分别对西塔0和西塔1求偏导后的函数
33 J_Theta0 += -(1/m) * (y_data[j] - ((Theta1 * x_data[j]) + Theta0))
34 J_Theta1 += -(1/m) * (y_data[j] - ((Theta1 * x_data[j]) + Theta0)) * x_data[j]
35
36 J_Cost[i] = J_CostValue
37 #更新截距和梯度
38 Theta0 = Theta0 - (lr * J_Theta0)
39 Theta1 = Theta1 - (lr *J_Theta1)
40 '''
41 end
42 }
43 '''
44
45 return Theta0,Theta1,J_Cost
46
47lr = 0.1 #设置学习率
48Theta0 = 0 #截距相当于Theta0
49Theta1 = 0 #斜率,相当于Theta1
50epochs = 500 #最大迭代次数
51
52print("Starting Theta0={0},Theta1={1},error={2}".format(Theta0,Theta1,compute_error(Theta0,Theta1,X,Y)))
53
54print("Running")
55Theta0,Theta1,J_Cost = gradient_descent_runner(X,Y,Theta0,Theta1,lr,epochs)
56
57print("After {0} iterations Theta0={1},Theta1={2},error={3}".format(epochs,Theta0,Theta1,compute_error(Theta0,Theta1,X,Y)))
58
59# 画图
60plt.plot(X, Y,'b.')
61#也就是y的值k*x_data+b
62plt.plot(X, X * Theta1 + Theta0, 'r')
63plt.show()
同样的,利用神经网络也可以进行线性回归。
1b = np.ones(100).reshape(100,1)
2old_X = np.column_stack((old_X,b))
3
4# 利用torch计算梯度并进行权重的修改
5X = torch.tensor(old_X, dtype=torch.float, device=device)
6Y = torch.tensor(old_Y, dtype=torch.float, device=device)
7
8# pytorch
9w1 = torch.randn(2, 1, device=device, dtype=dtype, requires_grad=True)
10loss = 0
11
12learning_rate = 1e-4
13for t in range(500):
14 y_pred = X.mm(w1).clamp(min=0)
15 # Compute and print loss using operations on Tensors.
16 # Now loss is a Tensor of shape (1,)
17 # loss.item() gets the scalar value held in the loss.
18 loss = (y_pred - Y).pow(2).sum()
19 if t % 100 == 99:
20 print(t, loss.item())
21
22 # 利用torch进行反向传播自动更新梯度
23 loss.backward()
24
25 with torch.no_grad():
26 # 更新权重向量,也就是ax+b 的a,b值
27 w1 -= learning_rate * w1.grad
28
29 # 将更新梯度清零
30 w1.grad.zero_()
31
32coefficient = torch.sum(w1,1)
33Theta1 = coefficient[0].item()
34Theta0 = coefficient[1].item()
35plt.figure()
36plt.scatter(X[:,0],Y,color='g',s=10) #X1 为横坐标轴值,y为纵坐标值
37plt.plot(X,Theta1 * X + Theta0,color='r',linewidth=2.5,linestyle='-')
38plt.show()